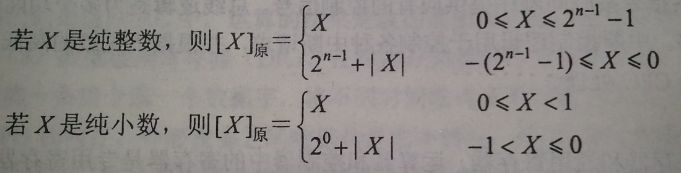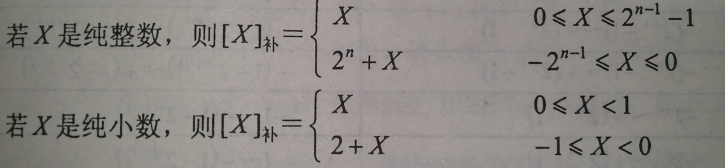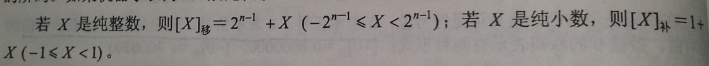本文共 2643 字,大约阅读时间需要 8 分钟。
原码
PS:正数的原、反、补码都一样:0的原码跟反码都有两个,因为这里0被分为+0和-0。
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值.
比如如果是8位二进制:
[+1]原 = 0000 0001 [-1]原 = 1000 0001例如: X=+101011 , [X]原= 00101011 X=-101011 , [X]原= 10101011
反码
反码的表示方法是:
* 正数的反码是其本身 * 负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.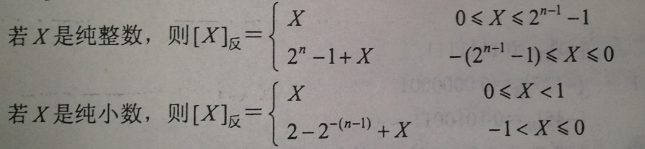
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
补码
补码的表示方法是:
* 正数的补码就是其本身 * 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1) * 更简单的方法是,符号位不变,从最低位开始,指导遇见第一个1,这个1后面的都不变,前面的所有位依次取反。0的补码是唯一的,如果机器字长为8那么[0]补=00000000。
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
移码
移码(又叫增码)是符号位取反的补码,一般用做浮点数的阶码,引入的目的是为了保证浮点数的机器零为全0。
8位光从移码本身来说,从00000000到11111111,由于其顺序就表示了从小到大的顺序,所以为0~255,但其真值表示范围为-128~127
在短浮点数表示中,移码为0~255,但是正常情况下,要表示无穷大以及其他的一些特殊值,0和255留作它用,所以E正常范围为1~254,在-127,所以为-126~127
例如:X=-101011 , [X]原= 10101011 ,[X]反=11010100,[X]补=11010101,[X]移=01010101
为何要使用原码, 反码和补码
所以补码的设计目的是:
⑴使符号位能与有效值部分一起参加运算,从而简化运算规则. ⑵使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计 所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、C等其他高级语言中使用的都是原码。现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别”符号位”显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在”0”这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
转载:http://blog.csdn.net/gatieme/article/details/50695785